Computational Mechanics & Artificial Intelligence Lab
Nick Napoleon Vlassis is an Assistant Professor in the Department of Mechanical & Aerospace Engineering at Rutgers University.
Home
About
Publications
Google Scholar
Hiring
Geometric Deep Learning for Computational Mechanics Part I: Anisotropic Hyperelasticity
Geometric Deep Learning for Computational Mechanics Part II: Graph Embedding for Interpretable Multiscale Plasticity
Sobolev Training of Thermodynamic-Informed Neural Networks for Interpretable Elasto-Plasticity Models with Level Set Hardening
Molecular Dynamics Inferred Transfer Learning Models for Finite-Strain Hyperelasticity of Monoclinic Crystals: Sobolev Training and Validations Against Physical Constraints
Component-Based Machine Learning Paradigm for Discovering Rate-Dependent and Pressure-Sensitive Level-Set Plasticity Models
Denoising diffusion algorithm for inverse design of microstructures with fine-tuned nonlinear material properties
nick.vlassis@rutgers.edu
Geometric Deep Learning for Computational Mechanics Part I: Anisotropic Hyperelasticity
Vlassis, Ma, Sun, CMAME, 2021.
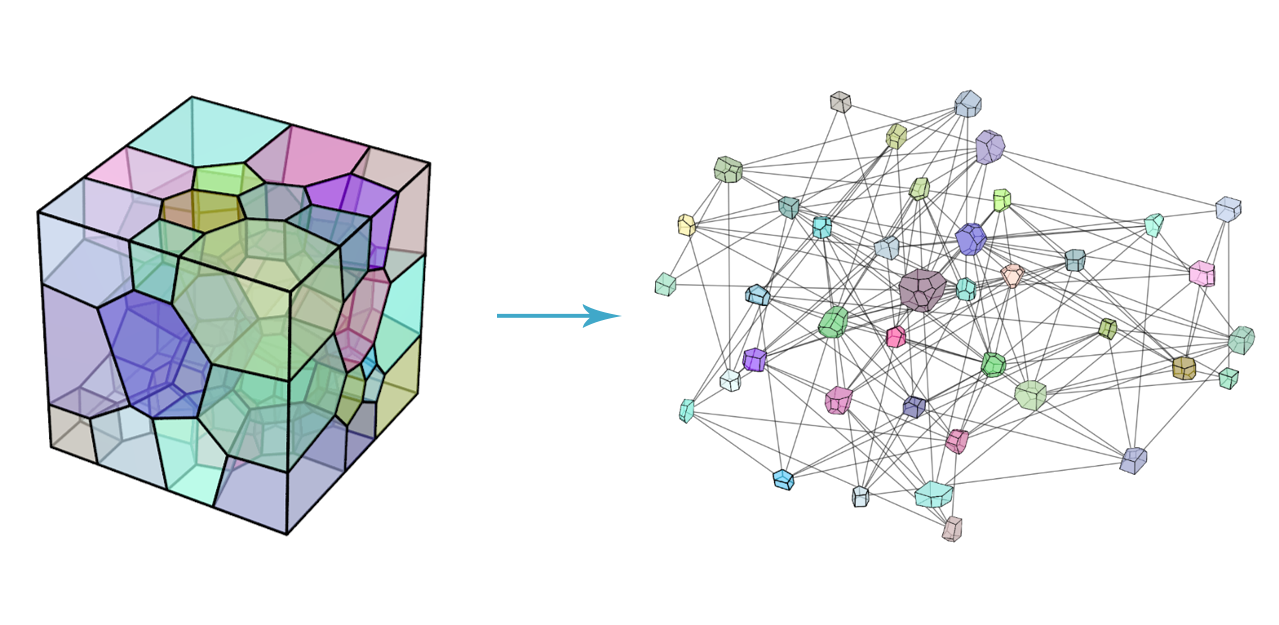
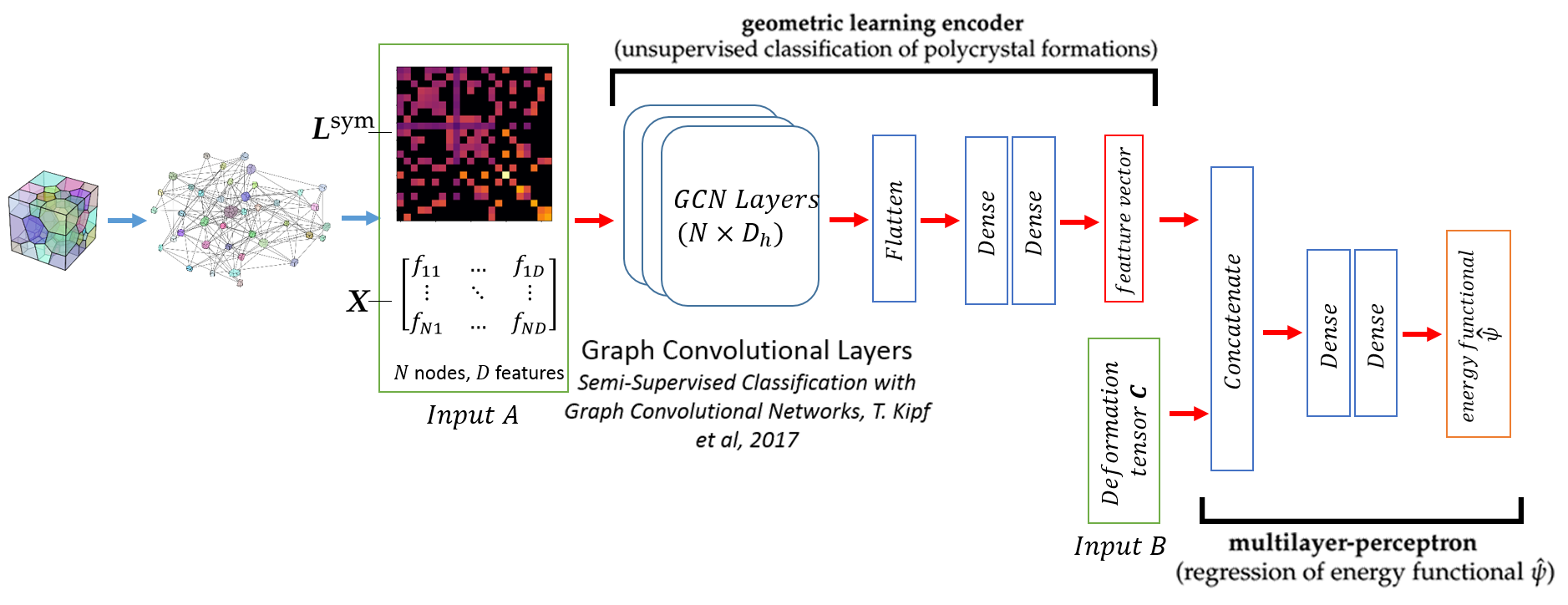
We developed a machine learning approach that combines geometric deep learning and Sobolev training to generate a family of finite strain anisotropic hyperelastic models to predict the homogenized responses of polycrystals not seen during training. We use a weighted graph as a new high-dimensional descriptor to represent topological information, such as the connectivity of anisotropic grains in an assemble, and a graph convolutional deep neural network to extract low-dimensional features and learn the influence on the stored elastic energy functionals. We use Sobolev training to ensure smoothness and accuracy in predictions, and results from numerical experiments show improved predictions compared to classical training methods.
Read more →
Read more →
