Computational Mechanics & Artificial Intelligence Lab
Nick Napoleon Vlassis is an Assistant Professor in the Department of Mechanical & Aerospace Engineering at Rutgers University.
Home
About
Publications
Google Scholar
Hiring
Geometric Deep Learning for Computational Mechanics Part I: Anisotropic Hyperelasticity
Geometric Deep Learning for Computational Mechanics Part II: Graph Embedding for Interpretable Multiscale Plasticity
Sobolev Training of Thermodynamic-Informed Neural Networks for Interpretable Elasto-Plasticity Models with Level Set Hardening
Molecular Dynamics Inferred Transfer Learning Models for Finite-Strain Hyperelasticity of Monoclinic Crystals: Sobolev Training and Validations Against Physical Constraints
Component-Based Machine Learning Paradigm for Discovering Rate-Dependent and Pressure-Sensitive Level-Set Plasticity Models
Denoising diffusion algorithm for inverse design of microstructures with fine-tuned nonlinear material properties
nick.vlassis@rutgers.edu
Component-Based Machine Learning Paradigm for Discovering Rate-Dependent and Pressure-Sensitive Level-Set Plasticity Models
Vlassis, Sun, JAM, 2021.
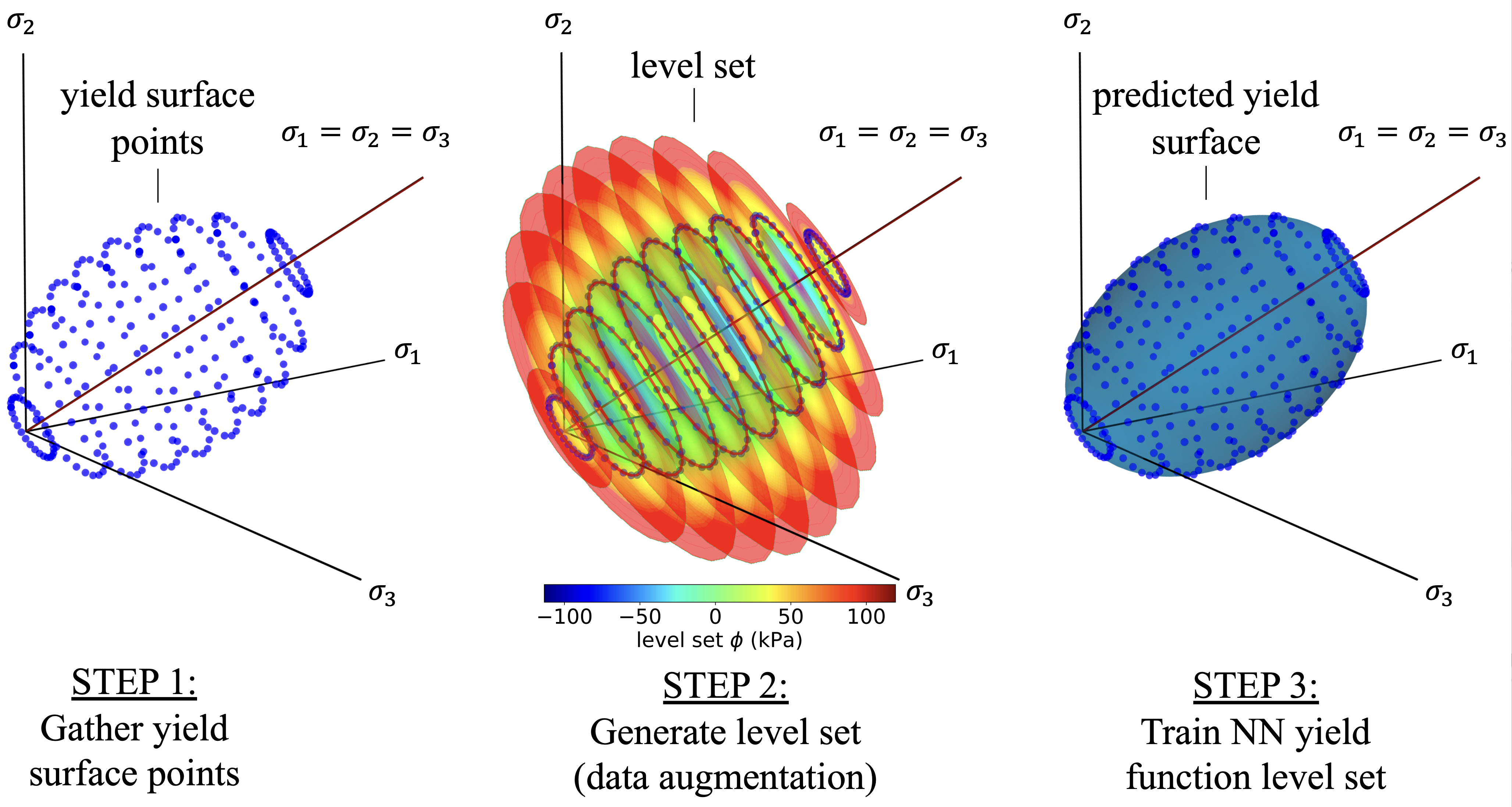
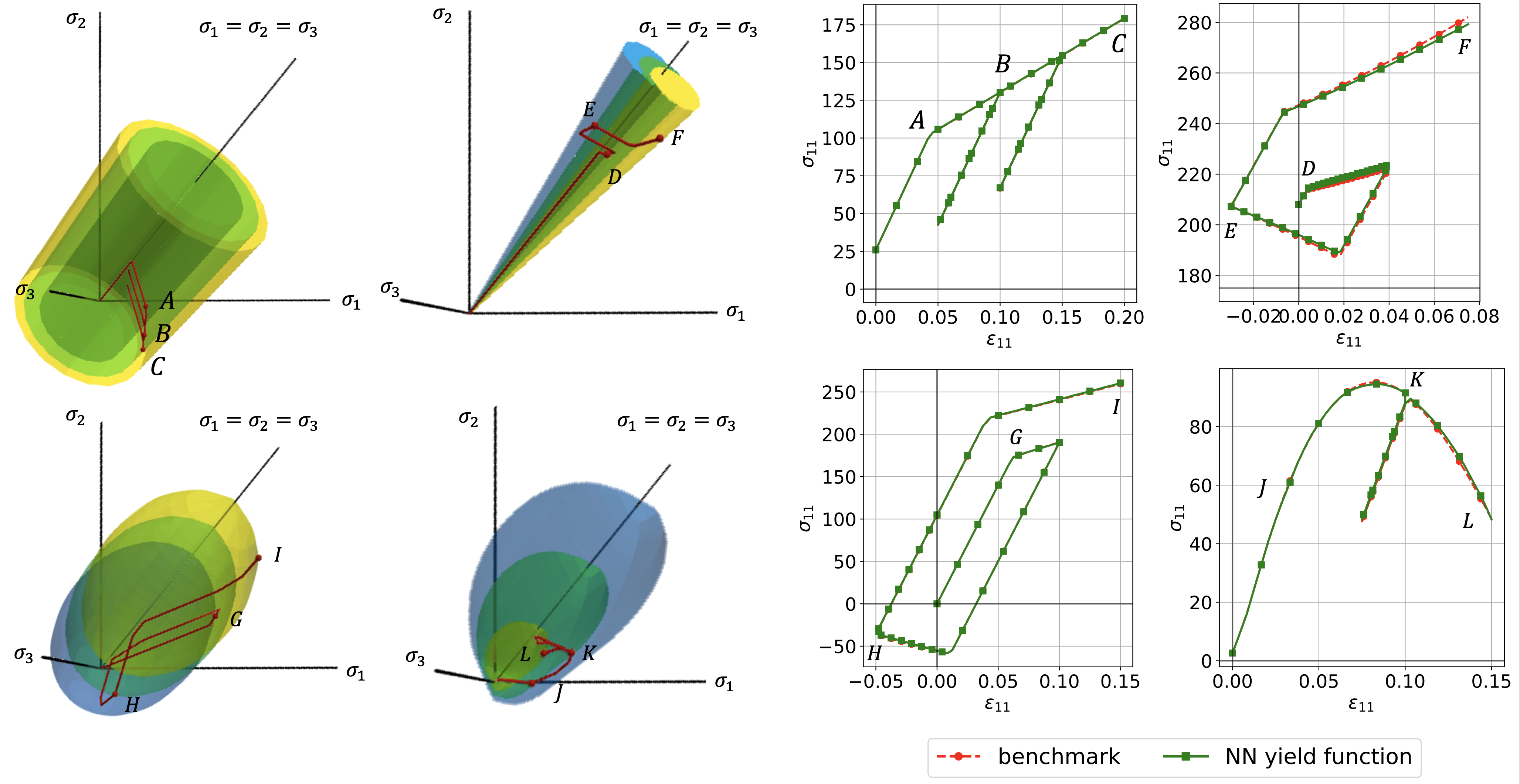
Conventionally, neural network constitutive laws for path-dependent elastoplastic solids are trained via supervised learning performed on recurrent neural networks, with the time history of strain as input and the stress as output. However, training neural networks to replicate path-dependent constitutive responses requires significantly more data due to the path dependence. This demand on diversity and abundance of accurate data, as well as the lack of interpretability to guide the data generation process, could become major roadblocks for engineering applications. In this study, we attempt to simplify these training processes and improve the interpretability of the trained models by breaking down the training of material models into multiple supervised machine learning programs for elasticity, initial yielding, and hardening laws that can be conducted sequentially. To predict pressure sensitivity and rate dependence of the plastic responses, we reformulate the Hamliton–Jacobi equation such that the yield function is parametrized in a product space spanned by the principal stress, the accumulated plastic strain, and time. To test the versatility of the neural network meta-modeling framework, we conduct multiple numerical experiments where neural networks are trained and validated against (1) data generated from known benchmark models, (2) data obtained from physical experiments, and (3) data inferred from homogenizing sub-scale direct numerical simulations of microstructures. The neural network model is also incorporated into an offline FFT-FEM model to improve the efficiency of the multiscale calculations.
Read more →
Read more →
